一次型解决超前进位加法器——32位CLA的实现

网上现有的资料，虽然很多，但是要么杂乱无章，要么不成体系。本来我觉得是很简单的一个问题，看了一圈下来，半小时过去竟然还是云里雾里。一怒之下，翻开我本科计组课件，花了几分钟浏览了一下，顿感拨云见日，浑身舒爽。
超前进位加法器的核心思想是并行计算进位位，我们想要超前计算的就是进位信号C，这个思想将会贯彻加法器的设计始终，从最初的4bitCLA到16bitCLA组间进位都体现了这个思想。
我们先从最简单的一位全加器开始说起，观察普通一位全加器的逻辑表达式：
\[ \left\{ \begin{array}{l} s=a\oplus b\oplus c ,\\ c_{out}=ab+c_{in}(a\oplus b) \end{array} \right. \]

其中a与b是两个加数、\(c_{in}\)是低位进位信号、s是和数、\(c_{out}\)是高位进位，这里的五个信号都是1bit的。由于进位是由低位向高位逐级传递，进位的逻辑形似链条，所以将进位传递逻辑叫做进位链Carry Link。我们可以看出，如果将位数从一位扩展到多位，高位进位信号总是依赖低位进位信号的，这就会造成非常可观的延迟，运算速度与进位传递速度有关。于是又引入了数字IC设计中亘古不变的话题，面积与速度的tradeoff，只不过这次我们是用面积换速度，即使用更复杂的电路设计换取更快的运行速度。
人们开始想办法优化电路结构，提取其共有部分： \[ \left\{ \begin{array}{l} P=a\oplus b ,\\ G=ab \end{array} \right. \] 这里的a与b是输入的待求和数据，即可以是1bit的也可以是N bits的数据。
于是，对于N位超前进位加法器，进位与求和的逻辑表达式可以重新写成如下形式：
\[ \left\{ \begin{array}{l} s_i=Pi \oplus c_{i-1}, & &i=1,...,N \\ c_i=G_i\oplus c_{i-1}P_i, & & i=1,...,N \\ c_0=c_{in} & & \\ c_{out}=c_N & & \end{array} \right. \] 其中： \[ \left\{ \begin{array}{l} P_i=a_i\oplus b_i, & &i=0,1,...,N-1 \\ G_i=a_ib_i, & &i=0,1,...,N-1 \end{array} \right. \] 写到这里，如果照着公式接着硬讲下去，那就又走上了网上其他人的老路，但我不想听你讲公式，能不能来点实际的、形象一点的、能让知识在不觉间水灵灵地流入我的脑子。

首先，从命名开始说起，难道大家就没有好奇P和G是怎么冒出来的？为啥不用L、M、N？这26个字母排着队地等着上呢，怎么就冒出个P和G？原来，G被称为进位生成（generate）函数，P被称为进位传递（propagate）函数，计组课件里有一张图我觉得十分形象（我为郑老师打call）：低位进位\(c_0\)与进位生成信号g都能产生进位信号，它们就像管道中的补水口，控制水的来源；而进位传递信号p则是一级级传递进位信号，它们则像是管道中的水阀，控制水的流通。

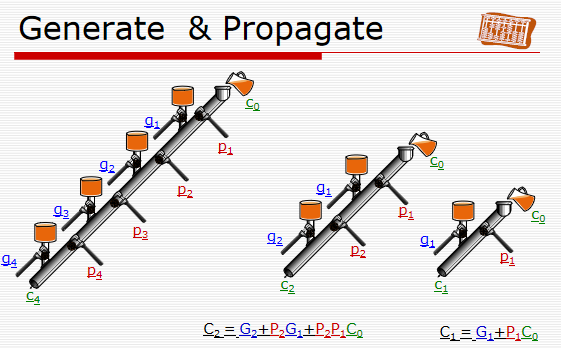
于是，进位信号就像水流一样在管道里被一级级的水阀放行，而且这个过程是并行的，一旦配置好进位链，你能同时得到c1、c2、c3等所有的进位信号，实现了超前进位，也就是提前计算好所有的进位信号。我们所需要做的仅仅就是配置好这个进位链，怎么配置？人家公式不都告诉你了：
\[ \left\{\begin{array}{l} P_i=a_i\oplus b_i, & &i=0,1,...,N-1 \\ G_i=a_ib_i, & &i=0,1,...,N-1 \end{array} \right. \] \[ \left\{\begin{array}{l} s_i=Pi \oplus c_{i-1}, & &i=1,...,N \\ c_i=G_i\oplus c_{i-1}P_i, & & i=1,...,N \\ c_0=c_{in} & & \\ c_{out}=c_N & & \end{array} \right. \]

如果仅仅是实现一个4bit的超前进位加法器，其示意图如下所示：

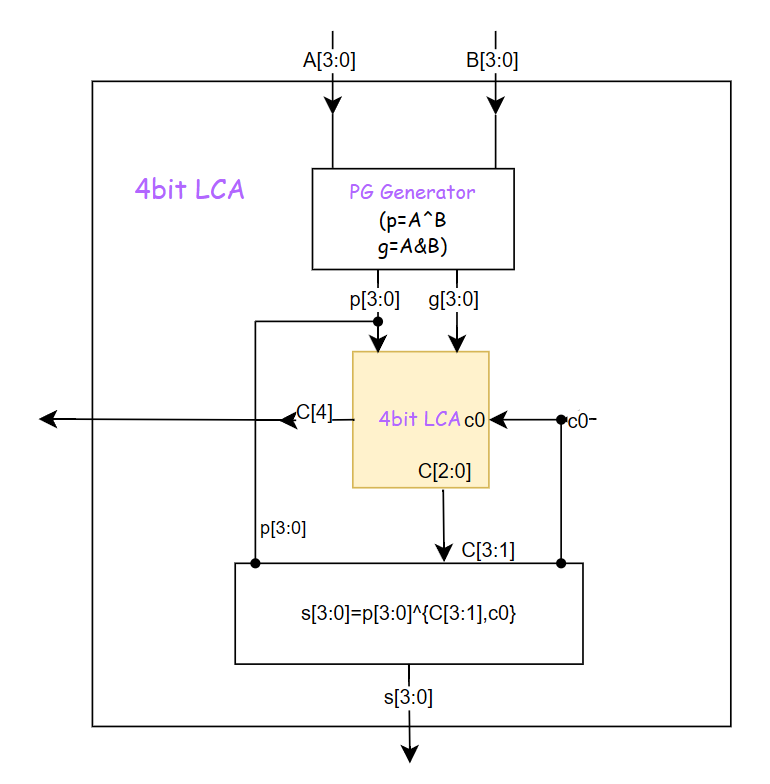
PG Generator用来产生P和G，其内部执行了下述操作： \[ \left\{\begin{array}{l} P_i=a_i\oplus b_i, & &i=0,1,...,N-1 \\ G_i=a_ib_i, & &i=0,1,...,N-1 \end{array} \right. \]

4bitCLA利用上面产生的P与G信号，生成进位信号c，其内部执行了下述操作： \[ \left\{\begin{array}{l} c_1=G_1+c_0P_1 \\ c_2=G_2+c_1P_2=G_2+(G_1+c_0P_1)P_2=G_2+G_1P_2+c_0P_2P_1 \\ c_3=G_3+c_2P_3=G_3+(G_2+G_1P_2+c_0P_1P_1)P_3=G_3+G_2P_3+G_1P_3P_2+c_0P_3P_2P_1 \\ c_4=G_4+c_3P_4=G_4+(G_3+G_2P_3+G_1P_3P_2+c_0P_3P_2P_1)P_4=G_4+G_3P_4+G_2P_4P_3+G_1P_4P_3P_2+c_0P_4P_3P_2P_1 \end{array}\right. \]

最后的和数由进位传递信号P与进位信号c异或得到，注意第四位进位信号\(c_4\)是高位进位，用来传递给下一级电路的，其计算逻辑如下： \[ \left\{\begin{array}{l} s_0=P_0\oplus c_0 \\ s_1=P_1\oplus c_1 \\ s_2=P_2\oplus c_2 \\ s_3=P_3\oplus c_3 \end{array}\right. \]

如果涉及到大位数的超前进位加法器——例如我想实现一个16bit超前进位器，还是使用上面的方法构建的话，会在进位链中引入超高扇入的逻辑门，使得整体电路规模以指数级增长。
为了控制超前进位电路的进位链复杂度，我们可以将一条较大的完整的超前进位链划分为多块较小的超前进位链块，也就是将16bitCLA分成4组4bitCLA，如下图所示：

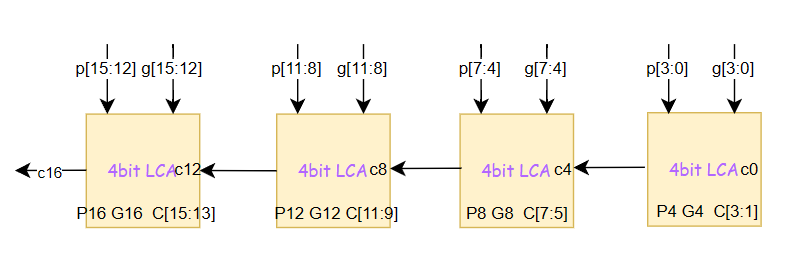
这就是最简单的组内超前进位、组间串行进位，也就是说每一个4bitCLA内部是超前进位的，而4组4bitLCA之间是串行进位的，\(c_4\)、\(c_8\)、\(c_{12}\)与\(c_{16}\)的产生不是并行的，\(c_4\)的产生依赖于第一组4bitLCA的\(c_0\)、\(c_8\)的产生依赖于第二组4bitLCA的\(c_4\)，以此类推。
于是就会产生一个疑问：能否实现组间并行进位？ 我们仔细分析一下\(c_4\)信号： \[ c_4=G_4+c_3P_4=G_4+(G_3+G_2P_3+G_1P_3P_2+c_0P_3P_2P_1)P_4=G_4+G_3P_4+G_2P_4P_3+G_1P_4P_3P_2+c_0P_4P_3P_2P_1 \] 发现它也能拆开为超前进位的形式： \[ \left\{\begin{array}{l} G_4^*=G_4+G_3P_4+G_2P_4P_3+G_1P_4P_3P_2 \\ P_4^*=P_4P_3P_2P_1 \end{array}\right. \]

我们把G4与P4称为成组进位信号，有了它俩，c4可以写成： \[ c_4=G_4^*+P_4^*c_0 \]

有意思的是，产生C4的逻辑与之前产生组内进位信号ci的逻辑表达式是一模一样的： \[ c_i=G_i\oplus c_{i-1}P_i,i=1,...,N \]

于是我们得出下面的结论：组内、组间并行进位链的逻辑形态完全相同
这个结论非常重要，这意味着我们在处理组间并行进位时可以完全复用原有的4bit CLA电路，只需要将原有4bitCLA模块中接入\(G_4^*\)、\(G_8^*\)、\(G_{12}^*\)、\(G_{16}^*\)、\(P_4^*\)、\(P_8^*\)、\(P_{12}^*\)、\(P_{16}^*\)即可产生之前需要串行等待的\(c_4\)、\(c_8\)、\(c_{12}\)与\(c_{16}\)，降低了延时的同时也没有增加额外的设计，因为我们还是复用了原有的CLA电路，只是增加了硬件资源开销，没有增加设计开销。
于是，改进之后的电路如下图所示：

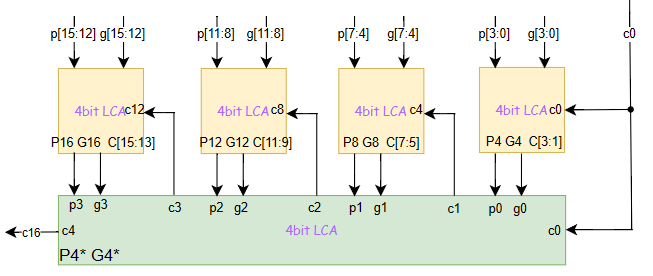
简洁起见，上面4个CLA中的成组进位信号我没加*，我们心里知道那是成组进位信号就行了。
扩展到32bitCLA的设计，也是这个道理，我们先来看组间串行进位的32bitCLA：

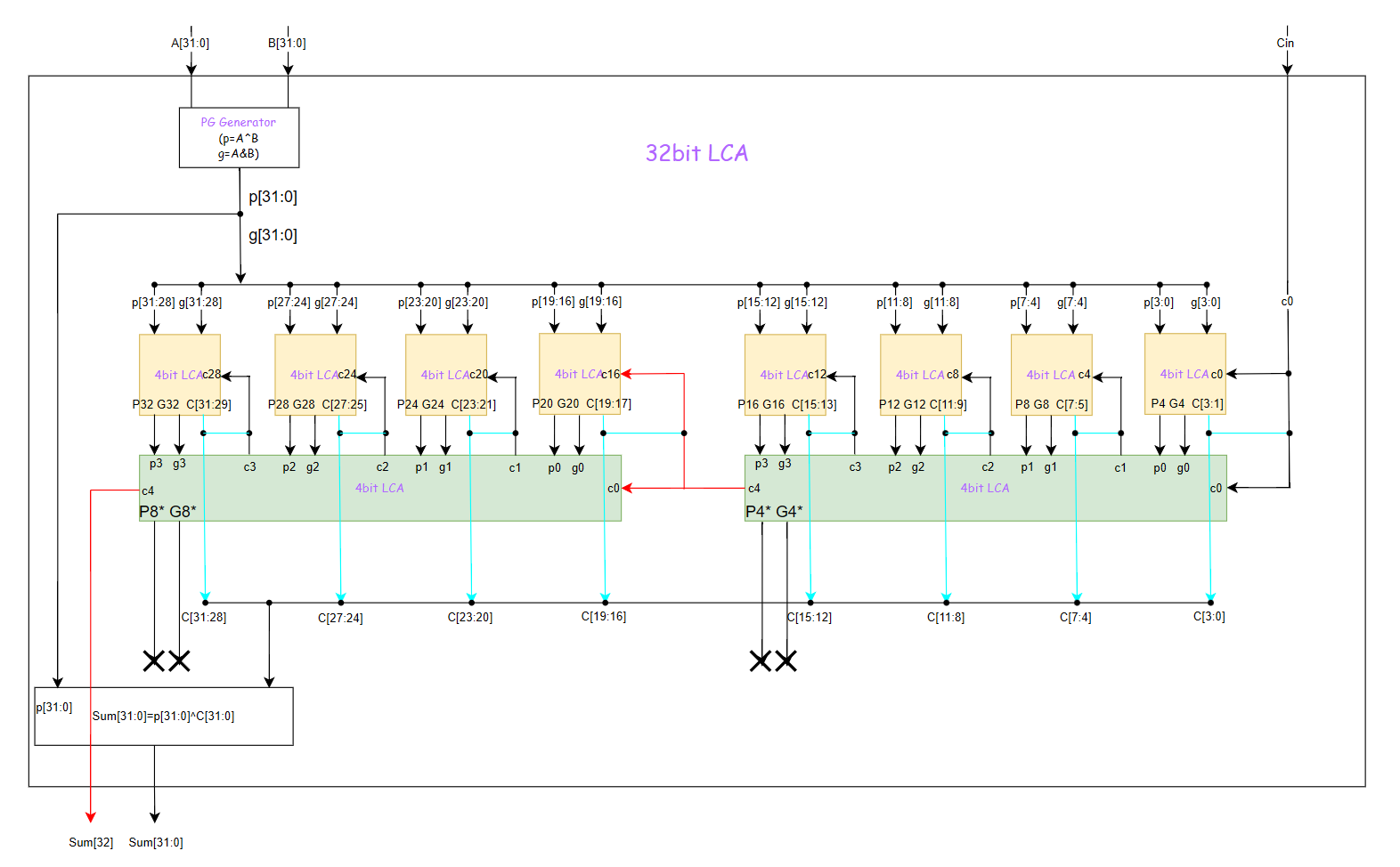
图中标蓝色部分表示生成的4bit进位信号有3bit来自CLA，1bit来自地位进位，是二者的组合；图中标红色部分表示着组间串行进位。
超前进位的思想同样可以应用到图中两个标红色部分的进位链信号的产生与传递，所以我们可以将闲置的\(P_4^*G_4^*\)与\(P_8^*G_8^*\)利用起来，再额外使用一个4bitCLA来产生这两个进位信号，如下所示：

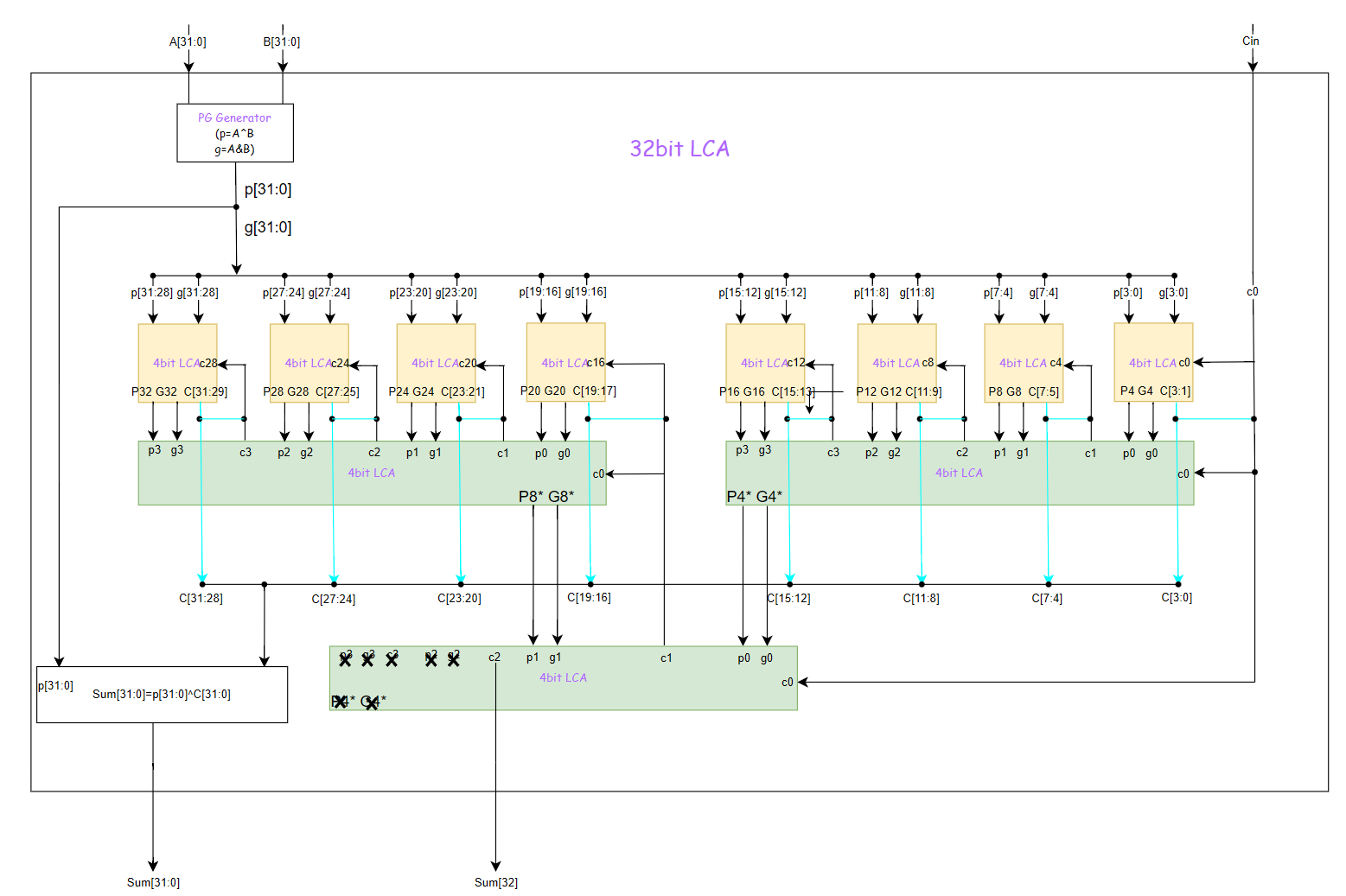
最后贴出verilog代码供大家参考：

module add_cla_4_4(
    input   wire    [3:0]   p,
    input   wire    [3:0]   g,
    input   wire            cin,

    output  wire            P,      //组间进位信号（成组进位信号）
    output  wire            G,      //组间进位信号（成组进位信号）
    output  wire    [2:0]   cout    //第四位cout信号被拆分为P与G
);

    assign P = p[3]&p[2]&p[1]&p[0];
    assign G = g[3]|(p[3]&g[2])|(p[3]&p[2]&g[1])|(p[3]&p[2]&p[1]&g[0]);

    assign cout[0] = g[0]|(p[0]&cin);
    assign cout[1] = g[1]|(p[1]&g[0])|(p[1]&p[0]&cin);
    assign cout[2] = g[2]|(p[2]&g[1])|(p[2]&p[1]&g[0])|(p[2]&p[1]&p[0]&cin);
    // assign cout[3] = g[3]|(p[3]&g[2])|(p[3]&p[2]&g[1])|(p[3]&p[2]&p[1]&g[0])|(p[3]&p[2]&p[1]&p[0]&cin);
    // cout[3] = P|G&cin;
endmodule

module add_cla_32_32
(
    input   wire    [31:0]   A,
    input   wire    [31:0]   B,

    output  wire    [32:0]   Sum
);

wire [31:0] p;
wire [31:0] g;
wire [31:0] c;
wire c_x;

wire [9:0]  P;
wire [9:0]  G;

assign c[0] = 1'b0;
assign p = A^B;
assign g = A&B;

add_tc_4_4 add_tc_4_4_inst0_0(.p(p[3:0]),.g(g[3:0]),.cin(c[0]),.P(P[0]),.G(G[0]),.cout(c[3:1]));
add_tc_4_4 add_tc_4_4_inst0_1(.p(p[7:4]),.g(g[7:4]),.cin(c[4]),.P(P[1]),.G(G[1]),.cout(c[7:5]));
add_tc_4_4 add_tc_4_4_inst0_2(.p(p[11:8]),.g(g[11:8]),.cin(c[8]),.P(P[2]),.G(G[2]),.cout(c[11:9]));
add_tc_4_4 add_tc_4_4_inst0_3(.p(p[15:12]),.g(g[15:12]),.cin(c[12]),.P(P[3]),.G(G[3]),.cout(c[15:13]));
add_tc_4_4 add_tc_4_4_inst0_4(.p(P[3:0]),.g(G[3:0]),.cin(c[0]),.P(P[4]),.G(G[4]),.cout({c[12],c[8],c[4]}));

add_tc_4_4 add_tc_4_4_inst1_0(.p(p[19:16]),.g(g[19:16]),.cin(c[16]),.P(P[5]),.G(G[5]),.cout(c[19:17]));
add_tc_4_4 add_tc_4_4_inst1_1(.p(p[23:20]),.g(g[23:20]),.cin(c[20]),.P(P[6]),.G(G[6]),.cout(c[23:21]));
add_tc_4_4 add_tc_4_4_inst1_2(.p(p[27:24]),.g(g[27:24]),.cin(c[24]),.P(P[7]),.G(G[7]),.cout(c[27:25]));
add_tc_4_4 add_tc_4_4_inst1_3(.p(p[31:28]),.g(g[31:28]),.cin(c[28]),.P(P[8]),.G(G[8]),.cout(c[31:29]));
add_tc_4_4 add_tc_4_4_inst1_4(.p(P[8:5]),.g(G[8:5]),.cin(c[16]),.P(P[9]),.G(G[9]),.cout({c[28],c[24],c[20]}));

add_tc_4_4 add_tc_4_4_inst2(.p({2'b00,P[9],P[4]}),.g({2'b00,G[9],G[4]}),.cin(c[0]),.P(),.G(),.cout({c_x,Sum[32],c[16]}));

assign Sum[31:0] = p^c;
    
endmodule

Modelsim仿真结果如下图，我使用的是xilinx的zynq7020也就是xc7z020clg400-1这块片子：

图 8 逻辑资源占用

图 9 功耗仿真

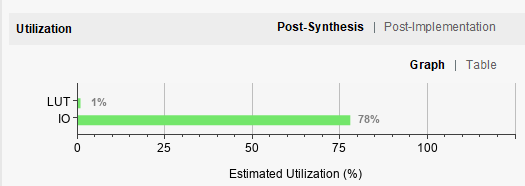
可以看出逻辑是正确的，但由于没有绑定IO端角，所以导致On-Chip Power有些大。