群时延相时延

引子：咋又是你，群时延？

今天在看通信原理时，又碰到了群时延这个老朋友，之前在看信号与系统与射频集成电路基础时就没怎么弄明白，今儿个又让我给遇上了，俗话说再一再二不再三，今天必须把它给解决掉。查了很多资料，又翻出了之前信号与系统，写得那叫一个obscure，又费了很大功夫查资料，终于弄明白了。

辨析：好像有个弟弟叫相时延？

首先要明确的概念是，时延代表的含义是什么——时间上的延迟。那么时间与相位又该如何联系上？我们很自然地联想到时间与相位之间的关系：
\[ \theta = \omega·t \] 式中\(\theta\)代表相位，单位rad；\(\omega\)代表角频率，单位rad/s；t代表时间，单位s。 我们把\(\Delta\theta=\theta\left(t_1\right)-\theta\left(t_2\right)=\omega\left(t_1-t_2\right)\)称为相位延迟（相移，phase shift），用\(\varphi\left(\omega\right)\)、∠Hjω表示，单位是rad；将\(-\frac{\varphi\left(\omega\right)}{\omega}\)、\(-\frac{\angle H\left(j\omega\right)}{\omega}\)称为相位延时（相时延，phase delay），用\(P\left(\omega\right)\)表示，单位是s。 既然相时延的公式中又有相位，又有频率，又涉及到斜率，可以使用bode图来清晰查看相时延，因为系统相频响应的bode图横坐标就是\(\omega\)，纵坐标就是\(\angle H\left(j\omega\right)\)。考虑以下两种系统的相频响应bode图：

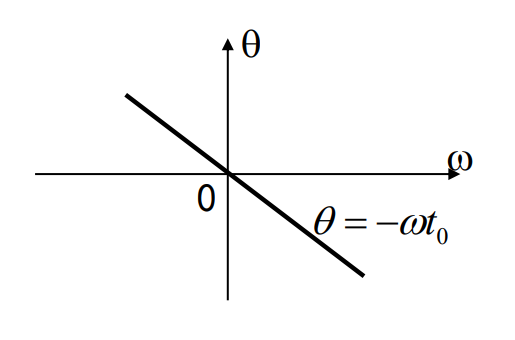
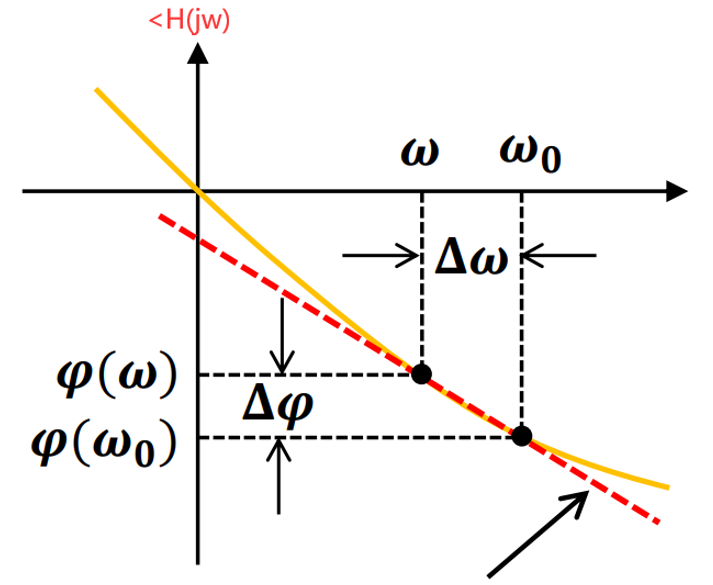
可以看出，对于图1所示线性相位系统，还好说，其相频响应bode图斜率的相反数就是相时延，一旦迁移到非线性相位系统，相时延\(P\left(\omega\right)=-\frac{\angle H\left(j\omega\right)}{\omega}\)似乎就没什么实际意义了，可是转念一想：诶呀，群时延是线性相位系统bode图的斜率，那我只要再弄一个非线性系统bode图的斜率不就好了？图像斜率用什么表示？不就是微分嘛。于是乎，群时延的概念应运而生，定义群时延：
\[ \tau(\omega) = -\frac{d\angle H(j\omega)}{d\omega} \]

表示信号经过系统后，对于信号处于不同频率成分\(\mathbf{\omega}\)的分量，它们各自的相位所经历的时间上的延时。
从上述定义我们可以看出，相时延就是群时延在线性相位系统下的特殊情况，也就是相频响应bode图斜率为定值，此时\(-\frac{d\angle H\left(j\omega\right)}{d\omega}=-\frac{\angle H\left(j\omega\right)}{\omega}\)。写到这里，不由得想起来初中对速率的定义是\(v=\frac{s}{t}\)，而上了高中，学了微积分之后，速率的定义式就变成：\(v=\frac{ds}{dt}\)，原来是因为初中研究的都是恒速率简单运动，而高中研究的就是稍复杂些的变速率运动，于是乎，前者对速率的定义不再适用（或者说变成了平均速率），后者对速率的定义更为精确（也就是瞬时速率）。所以说，相时延与群时延的区别就好比平均速率与瞬时速率之间的区别，这么一说是不是好懂了许多？

缘由：为什么需要群时延

有了上面对群时延的定义，我们不经联想到：啥啊这是？一上来就噼里啪啦一堆定义，干啥玩意啊，有啥用啊？那当然是研究一个信号经过系统后的失真情况。
我们考虑一个方波，如果是一个连续时间周期信号，那么它是由无数个复指数信号（正弦波）叠加而成（连续时间周期信号的傅里叶级数是一般一个周期序列，这里不详细展开，详见《信号与系统》）。那么这些复指数信号在通过一个系统后，要想输出还是一个方波，即形状不发生改变，就要求它们在时域上的相对位置不能变化，也就是所有频率的波的延迟时间一致。等会，“所有频率的波的延迟时间”，不就是群时延的定义吗？
音乐厅中，我们希望不同频率声音到达听众耳朵的时间延迟是相等的，以减小声音的失真此时就要求线性相位系统；雷达系统中，回波信号的处理若不满足线性相位，则会给举例计算带来误差。
如果系统对所有的频率分量都有相同的相位延时（线性相位系统，此时群时延等于相时延，相频响应曲线为一条直线），那么信号经过该系统后，波形不发生失真，只是有一定的延时。但如果不同频率分量有不同的相位延时（非线性相位系统），那么信号经过该系统后将产生失真。当然这里所说的失真是指相位失真，如果信号还想要不发生幅度失真，那么它的幅频响应也得是一条水平直线才行。

注：
数字角频率\(\omega\)等于模拟角频率\(\Omega\)对采样频率\(f_s\)归一化，即：1 \(\omega=\frac{\Omega}{f_s}=\Omega T_s\)，单位rad；其中\(T_s\)为采样周期，单位s；\(\Omega=2\pi f\)，单位rad/s；