乘法器优化——Booth编码的奥秘

引子：乘法器概论

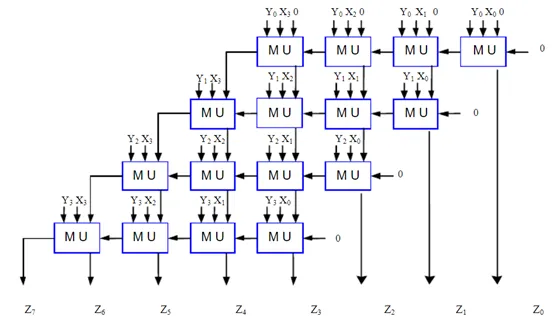
在整个数字集成电路的世界里，乘法器的速度优化是一个亘古不变的话题，因为乘法器是高性能微处理器中的关键部件，是进行高速计算特别是信号处理等方面应用时所必须的。对于现今普遍采用的阵列乘法器（array multiplier），它囊括了以下三个功能：产生部分积、累积部分积与最终相加，所以在进行乘法器速度优化时，我们可以从以下三个方面考虑：

• 加快部分积的产生
• 减少部分积的数
• 加速部分积的加法操作

图 1 二进制阵列乘法器

本文主要在查阅有关资料的基础上，整理了布斯编码（Booth Encoding一种用来减少部分积数目的算法）与在此基础上提出的改进布斯编码（modified Booth’s encoding）的相关知识，并结合自己的理解，使用通俗易懂的语言进行阐述。

Booth编码

Wikipedia定义

布斯编码可以减少部分积的数目，用来计算有符号乘法，提高乘法运算的速度。对于Booth编码，维基百科是这么说的：
这段详解已经胜过国内大多数教材的介绍，但相信这一大串数学符号也会劝退很多人，本文的目的就是通俗易懂，让小白也能看懂Booth编码。所以我又查阅资料，重新进行整理。
锵！且听我娓娓道来~

工作原理

我们知道，乘法计算本质上就是加法运算，但当乘数中二进制1数量过多时，会出现大量繁杂的加法运算，而二进制0的存在可以降低运算次数，因为0和任何数相乘都为0，我们就无需再进行计算，就像下图中这样：
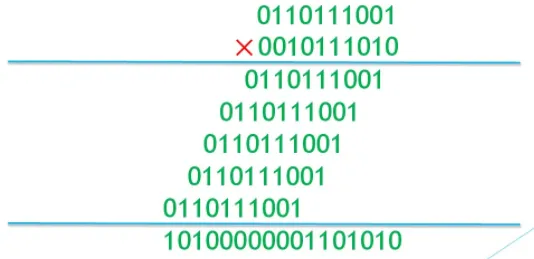可以看出，相较于图4，图3中的计算由于乘数中0的个数较多，使得计算大大简化。
那么问题来了，是否存在这样一种编码方式，能够大大缩减乘数中二进制1的个数，进而简化运算？答案是肯定的，也就是我们将要介绍的Booth编码。
其实早在小学时代，我们就学过这样的简便运算：

9x99=9x(100-1)=900-9=891

将乘数“99”化为“100-1”，计算更为简单。类似的，在二进制补码乘法XY中，我们也可以采取相同的操作。对于乘数:
\[ Y=[0111\_1110]_补=2^6+2^5+2^4+2^3+2^2+2^1 \]
我们采用另外一种相对简单的表示方式：
\[ [0111\_1110]_补=[1000\_0000]_补-[0000\_0010]_补，将其记为[1000\_00\overline10]（这里的\overline1是-1的缩写符号） \] 此时XY可以表示为：
\[ X*Y=X*[0111\_1110]_补=X*([1000\_0000]_补-[0000\_0010]_补)=X*[1000\_0000]_补-X*[0000\_0010]_补 \]
采用这一形式，我们只需相加两个部分积（但这要求最终设计的加法器必须也能执行减法，否则需将减法-[0000_0010]补转换成补码加法+[1111_1110]补，这又会产生七个部分积，得不偿失）。这种形式的变换称为布斯编码（Booth Encode），它使部分积的数目至少可以缩减到原来的一半。部分积的减少意味着相加次数的减少，从而加快了运算速度并减少了面积。

补码一位乘法

下面先简要阐述Booth算法的基本流程：
设\[[X]_补=x_s·x_1·x_2···x_n,[Y]_补=y_s·y_1·y_2···y_n\] 其中\(x_s,y_s\)均为符号位将符号位参与计算，运算数以补码表示且被乘数与部分积都取双符号位。

• 被乘数和部分积均取两位符号位即变形码，乘数取一位符号位，并参与运算
• 乘数末尾增设附加位\(Y_{n+1}\) ，其初始值为0。 \(Y_n\)和\(Y_{n+1}\)构成各步运算的乘数判断位，按表所示方法进行操作
• 按补码移位规则：部分积为正(第一符号位为0)，右移时有效位最高位补0；部分积为负，右移时有效位最高位补1
• 按Booth乘法表算法进行到第n+1步，但第n+1步的部分积不再移位

Booth乘法表
乘数位	编码位
00	0
01	+被乘数
10	-被乘数
11	0

下面给出一个示例：
设机器字长为5位，其中一位是符号位。且：\([X]_补=1.0101,[Y]_补=1.0011\)

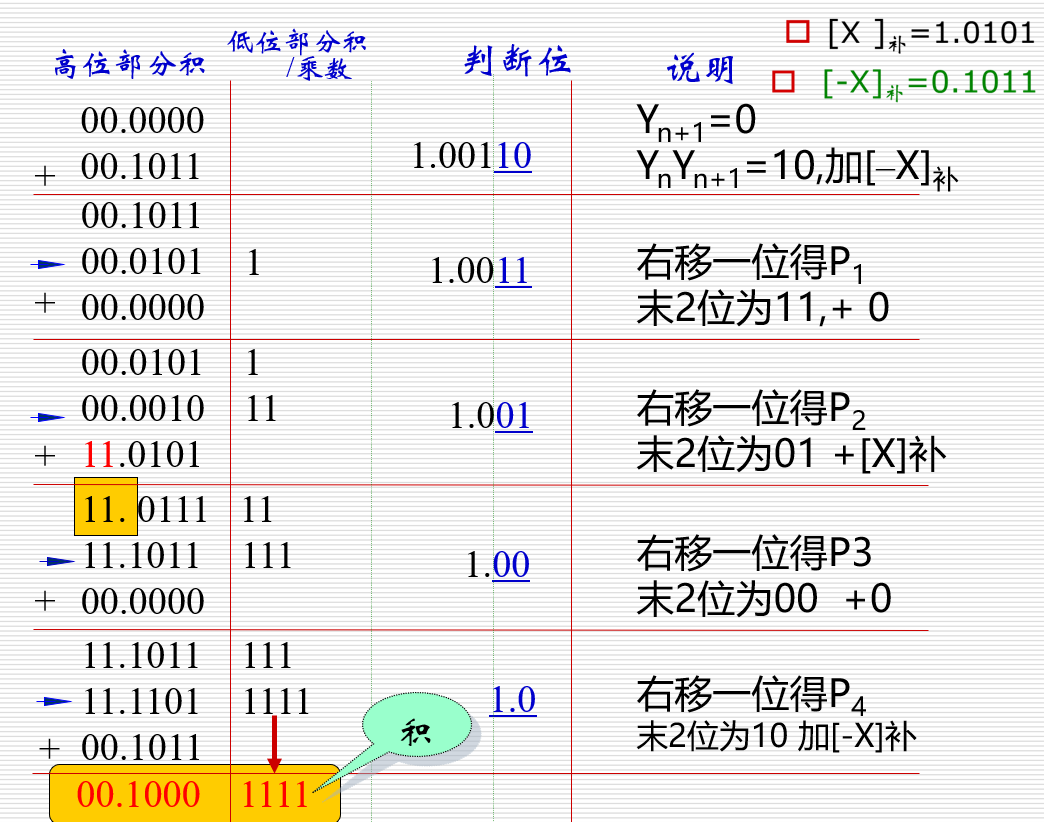
数学推导

对于只想浅探Booth编码的定义及工作原理的朋友，上述内容已足够清晰明了。但考虑到严谨性与实际应用，该部分给出部分数学上的推导以及更为详尽的说明。
前面已经提到将乘数\(Y=[0111\_1110]_补\)表示为\([1000\_00\overline10]\)，这个转换不是一眼看出来的，怎样将其进行推广，使我们能够对任意的乘数都能进行类似的转换以化简运算呢？
考虑有符号乘数： \[ Y=[y_{n-1}y_{n-2}···y_1y_0]_2 \]

\(Y=[y_{n-1}y_{n-2}···y_1y_0]_2\)
\((1)=-2^{n-1}·y_{n-1}+2^{n-2}·y_{n-2}+···+2^1·y_1+2^0·y_0+y_{-1}\)
\((2)=2^{n-1}·(y_{n-2}-y_{n-1})+2^{n-2}·(y_{n-3}-y_{n-2})+···+2^0·(y_{-1}-y_0)\)
\((3)=2^{n-2}·(y_{n-2}+y_{n-3}-2·y_{n-1})+2^{n-4}·(y_{n-4}+y_{n-5}-2·y_{n-3})+···+2^{0}·(y_{0}+y_{-1}-2·y_{1})\)
\((4)=\sum_{i=0}^{(N-1)/2}Y_i·4^i,(Y \in \{-2,-1,0,1,2\})\)

定义\(Y_i=y_{i-2}-y_{i-1}\)，考虑(2)式，对于二进制数\(Y,y_i \in \{0,1\}\) ，从(2)式中可以看出：
\[ \left\{ \begin{aligned} if & & y_{i+1}=y_i, & & then & & Y_i=0, \\ if & & y_{i+1}>y_i, & & then & & Y_i=1, \\ if & & y_{i+1}<y_i, & & then & & Y_i=-1. \end{aligned} \right. \] 这构成了Booth编码的部分积选择表。

Booth乘法表
乘数位	编码位
00	0
01	+被乘数
10	-被乘数
11	0

定义\(Y_i=y_{i-2}+y_{i-3}-2·y_{n-1}\)，考虑(3)式，对于二进制数\(Y,y_i \in \{0,1\}\) ，从(3)式中可以看出：
\[ \left\{ \begin{aligned} if & & y_{2i+1}=0 & & and & & y_{2i}+y_{2i-1}=0, & & then & & Y_i=0, \\ if & & y_{2i+1}=0 & & and & & y_{2i}+y_{2i-1}=1, & & then & & Y_i=1, \\ if & & y_{2i+1}=0 & & and & & y_{2i}+y_{2i-1}=2, & & then & & Y_i=2, \\ if & & y_{2i+1}=1 & & and & & y_{2i}+y_{2i-1}=0, & & then & & Y_i=-2, \\ if & & y_{2i+1}=1 & & and & & y_{2i}+y_{2i-1}=1, & & then & & Y_i=-1, \\ if & & y_{2i+1}=1 & & and & & y_{2i}+y_{2i-1}=2, & & then & & Y_i=0. \end{aligned} \right. \] 这构成了改进Booth编码的部分积选择表。

改进Booth乘法表
乘数位	编码位
000	0
001	+被乘数
010	+被乘数
011	+2×被乘数
100	-2×被乘数
101	-被乘数
110	-被乘数
111	0

同时，我们还从（4）中看出，改进的Booth编码相当于把乘数变换为一个四进制形式，而不是通常的二进制形式。

读者在这里可能会有些疑惑：为什么已有了Booth编码，还要研究一个改进的Booth编码？

这是因为，如果使用Booth编码，乘数经编码后含二进制1的数量是不确定的，这会导致产生不确定的部分积数目，在最坏情况下，一个8位的乘数经Booth编码后将含有4个部分积

考虑8位乘数在最坏情况下的输入：8位乘数1010_1010，经Booth编码后为\(\overline11\overline11\_\overline11\overline10=[0101\_0100]_补-[1010\_1010]_补\)，Rabaey书上原文的说法是:

“1010…10代表了最坏情况的乘数输入，因为它产生的部分积数目最多（为一半）”

在这个例子中体现为减数\([1010\_1010]_补\)在乘法运算时将会产生4个部分积。这里我有一点疑惑，按理说在乘法运算时将会产生7个部分积，被减数\([0101\_0100]_补\)将会产生3个部分积，减数\([1010\_1010]_补\)将会产生4个部分积。暂时保留这个疑惑，不求甚解了哈哈。

大小不同的部分积阵列对乘法器设计不合适，改进的Booth编码可以解决这个问题，正因如此，我们最常使用的是改进的Booth编码。

使用改进的Booth编码，乘数按三位一组进行划分，并相互重叠一位，每一组的三位按表改进的Booth编码表进行划分，（首先将乘数两两划分一组，那么编码的三位分别由当前组的两位加相邻低位组的最高位组成），编码过程由msb至lsb进行，编码后所形成的的部分积的数目等于乘数宽度的一半，是一个确定的数目。

最后给出一个改进Booth编码的示例：

考虑前面提及的8位二进制数\([0111\_1110]_补\)，按照改进Booth编码规则进行转换。首先将其两两划分一组，共分为四组：\(01、11、11、10\)。接着将当前组的两位与相邻低位组的最高位进行组合，分为这样四组：\(011、111、111、100\)，其中最后一组多出来的是附加位0。最后根据表11.2编码得到\(10(2×)、00(0×)、00(0×)、\overline10(-2×)\)，组合在一起表示为\(1000\_00\overline10\).这与前面采用Booth编码得到的结果是一致的。

小结

本文通过对乘法器的速度优化进行引入，以通俗易懂的语言，介绍了Booth编码及在此基础上提出的改进Booth编码的原理与示例。

后话

Booth编码是在本人学习计组、数集和硬件描述语言课程中反复碰到的一个概念，由于课程不做要求，一直没有太重视。但在数集的大作业中，其中一个选题又要求我们设计一个基于Booth编码的乘法器，虽然我没选这个（bushi）。因此我想要彻底弄懂这个概念，先后看了计组老师的PPT，啃了半天Rabaey的那本“圣经”，只觉头昏脑涨，查了很多资料才只敢说有一些浅显的了解，查阅资料加整理成markdown发布前后共耗费三天时间（markdown功底太差了，还得多练练）。由于本人能力与精力有限，文章难免存在错误与疏漏，大家还是有选择的阅读。

参考文献

[1].维基百科
[2].Rabaey. 数字集成电路——电路、系统与设计
[3].怎么理解Booth算法? - 知乎 (zhihu.com)
[4].计组课程PPT 定点原码-补码乘法器